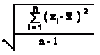L
LoudRed
OK, Now I'm totally confused about Cp/Cpk, Pp/Ppk. What I'm messed up on is what formulas to use, and what symbol is for which method.
What I'm messed up on is what formulas to use, and what symbol is for which method.
I know there are the two regular ways to calculate standard deviation. That is, using the "n" denominator for population SD, and "n-1" for sample SD. I also know there is a Sigma (Rbar/d2), and a Sigma-hat. Do either of these correspond to the two regular ways to calculate either Cp/Cpk or Pp/Ppk? If not then what are the formulas.
Also of interest to me concerns individual data and moving range.
Most of the data we've collected are individual data and not multiple readings for sub-group data. Below I've listed individual data for 30 pieces. At the point these data were taken, it was a population. I've attached an EXCEL file with all the data if you want to look at it along with my formulas. Please note that if you do, I only used the "mean - LSL" for my Cpk/Ppk formulas as all the data shows it to be in the bottom half of the spec.
L L Rng
1 79.4
2 79.9 0.5
3 80.7 0.8
4 81.2 0.5
5 81.2 0.0
6 82.5 1.3
7 81.2 1.3
8 80.5 0.7
9 81.5 1.0
10 80.7 0.8
11 80 0.7
12 81 1.0
13 80.3 0.7
14 80.7 0.4
15 80.9 0.2
16 80.7 0.2
17 81 0.3
18 81.7 0.7
19 82.2 0.5
20 81 1.2
21 81 0.0
22 80.8 0.2
23 81 0.2
24 79 2.0
25 83.5 4.5
26 80.2 3.3
27 80.4 0.2
28 79.8 0.6
29 80.2 0.4
30 78 2.2
Min 78.00 0
Max 83.50 4.5
Mean 80.74 0.91
Median 80.75
USL 100
LSL 70
Std. Dev (population) 1.013
Std. Dev (sample) 1.030
Std. Dev. Rbar/d2 0.455
Cp (Rbar/d2) 10.985
Cp (pop) 4.937
Pp 4.854
Cpk (Rbar/d2) 7.865
Cpk (pop) 3.535
Ppk 3.475
First of all, did I calculate using the correct formulas? If so, I don't understand why to use the SD (sample) for Pp/Ppk when that is taken from a population. I've also grouped the data into 15 subsets of 2, and 10 subsets of 3 and gotten the following results. Are these correct also?
If I've used all the correct formulas, then what I got for Cp/Cpk should use the (Rbar/d2) formulas, while thePp/Ppk uses the population SD (ie... "n" in the denominator). Please advise either way. For any assistance.....
I know there are the two regular ways to calculate standard deviation. That is, using the "n" denominator for population SD, and "n-1" for sample SD. I also know there is a Sigma (Rbar/d2), and a Sigma-hat. Do either of these correspond to the two regular ways to calculate either Cp/Cpk or Pp/Ppk? If not then what are the formulas.
Also of interest to me concerns individual data and moving range.
Most of the data we've collected are individual data and not multiple readings for sub-group data. Below I've listed individual data for 30 pieces. At the point these data were taken, it was a population. I've attached an EXCEL file with all the data if you want to look at it along with my formulas. Please note that if you do, I only used the "mean - LSL" for my Cpk/Ppk formulas as all the data shows it to be in the bottom half of the spec.
L L Rng
1 79.4
2 79.9 0.5
3 80.7 0.8
4 81.2 0.5
5 81.2 0.0
6 82.5 1.3
7 81.2 1.3
8 80.5 0.7
9 81.5 1.0
10 80.7 0.8
11 80 0.7
12 81 1.0
13 80.3 0.7
14 80.7 0.4
15 80.9 0.2
16 80.7 0.2
17 81 0.3
18 81.7 0.7
19 82.2 0.5
20 81 1.2
21 81 0.0
22 80.8 0.2
23 81 0.2
24 79 2.0
25 83.5 4.5
26 80.2 3.3
27 80.4 0.2
28 79.8 0.6
29 80.2 0.4
30 78 2.2
Min 78.00 0
Max 83.50 4.5
Mean 80.74 0.91
Median 80.75
USL 100
LSL 70
Std. Dev (population) 1.013
Std. Dev (sample) 1.030
Std. Dev. Rbar/d2 0.455
Cp (Rbar/d2) 10.985
Cp (pop) 4.937
Pp 4.854
Cpk (Rbar/d2) 7.865
Cpk (pop) 3.535
Ppk 3.475
First of all, did I calculate using the correct formulas? If so, I don't understand why to use the SD (sample) for Pp/Ppk when that is taken from a population. I've also grouped the data into 15 subsets of 2, and 10 subsets of 3 and gotten the following results. Are these correct also?
If I've used all the correct formulas, then what I got for Cp/Cpk should use the (Rbar/d2) formulas, while thePp/Ppk uses the population SD (ie... "n" in the denominator). Please advise either way. For any assistance.....